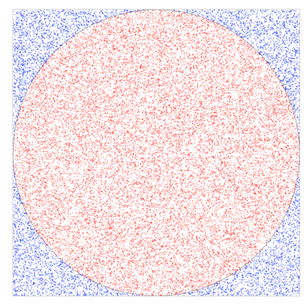
Her yıl Mart ayının 14'ü Pi günü (3.14) olarak kutlanır.
Bugün artık Uluslararası Matematik Günü olarak da kutlanacak. Pi günü kutlamaları çerçevesinde yapılabilecek aktiviteler ile ilgili internette birçok kaynak ve öneri var.
Ortaokul seviyesinde öğrencilerin en çok ilgisini çeken aktiviteleri aşağıda linkleri ile birlikte bulabilirsiniz.
Classroom Posters
UNESCO announced Pi-Day as the International Day of Mathematics in 2019.
"Greater global awareness of mathematical sciences is vital to addressing challenges in areas such as artificial intelligence, climate change, energy, and sustainable development, and to improving the quality of life in both the developed and the developing worlds."
Do not forget to check out the International Day of Mathematics Page for the posters!
2020 - Mathematics is Everywhere.
(The first-ever International Day of Mathematics)
2021 - Mathematics for a Better World.
2022 - Mathematics Unites.
2023 - Mathematics for Everyone